Based on the „normal“ ConvNets we try to explain the generalization of ConvNets. The background is, that an image can be seen as a graph and since our work focuses on finding structures in the Blockchain we need an approahce for generalizing ConvNets and applying them to arbitrary graphs.
Let’s have a look at the common known zero-padding ConvNets. We exclude in our approach narrow ones. It starts with convolution of the image. If we see pixels as nodes it results in a graph like the following (for a 3×3 pixels image):
 It illustrates an image as a graph where the neighbouring pixels have an edge. We generalize the image – now the graph – into a vector e of data entries:
It illustrates an image as a graph where the neighbouring pixels have an edge. We generalize the image – now the graph – into a vector e of data entries:
\(e = \left(\begin{array}{cc}A\\B\\C\\D\\E\\F\\G\\H\\I\end{array}\right)\) where each row corrensponds to a data entry.
It’s adjacency matrix looks like:
\(adj = \left(\begin{array}{cc}1 & 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0\\ 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0\\ 0 & 1 & 1 & 0 & 1 & 1 & 0 & 0 & 0\\1 & 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0\\1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\0 & 1 & 1 & 0 & 1 & 1 & 0 & 1 & 1\\0 & 0 & 0 & 1 & 1 & 0 & 1 & 1 & 0\\0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1\\0 & 0 & 0 & 0 & 1 & 1 & 0 & 1 & 1\\\end{array}\right)\)
Notes: The matrix’s columns and rows correspond to the nodes \(A,…,I\). So if the node A has an edge to node D then the matrix has a one in the 1st column and 4th row and also a one in the 4th columns and first row. So we have a symmetric matrix. Thus it contains redundancy which is important if we look at „only“ one specific node. The main diagonal contains 1, which means that the current node is also in the neighbourhood of itself. Further let’s extract the corresponding neighbourhood vector for a specific node. Let’s take node D. The corresponding neighbourhood vector looks like:
\(\left(\begin{array}{cc}1 & 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0\end{array}\right)\)
The intuition of this vector is to only look at the nodes which are neighbours of the specific node D. If we now create such a neighbourhood vector for every node we get n vectors where n is the number of nodes (it’s simply every row from the adjacency matrix). Ok, let’s stop here and look at the convolution itself.
The convolution in case of image ConvNets is the multiplication of a „small“ matrix with some pixels which are in the neighbourhood. We resolve the 2D convolution matrix to a weight vector w with m weights: \(w = \left(\begin{array}{cc}w_1& … & w_m\end{array}\right)\)
We assume now the above described image of 9 pixels where each pixel \(p_i \in \{1,2,3\}\). We convert the image to vector as described above which results in an example image:
\(e = \left(\begin{array}{cc}1\\2\\1\\1\\3\\2\\1\\1\\3\end{array}\right)\)
Generalized Convolution
We define the generalized convolution: \(C(x) = (w \otimes A^e) . e\) In the previous section we defined the weights and the vector e. Now we have to distribute the weights. For an easier understanding and to keep to data „small“ we define a small graph and a tiny weights to illustrate the concept. We define the following graph:
 With the following data entries:
With the following data entries:
\(e = \left(\begin{array}{cc}4\\ 5\\ 1\end{array}\right)\)
and some weights: \(w = (2, 1)\).
When we look at the formula above the term \(w \otimes A^e\) describes the convolution itself over the whole dataset (e.g. image) \(e\). To generate now all \(A^e\) matrices for the graph we have to build the neighbourhood matrices. E.g. in the neighbourhood of A is A and B. Note: Think about the convolution of an image, for an image (x,y) you take all pixels in the area of (x,y) into account AND also the pixel (x,y) itself. To go gurther the matrix \(A^e\) is no built like the following: number of columns is \(|e|\), in our case 3; number of rows is \(|w|\) in our case 2. The number of matrices we have to build is the triangular number (\(tn(n)\)) of the number of vertexes – 1: \(\frac{n(n+1)}{2}\) where \(n = 3 – 1 = 2\) in our case (this is simply the amount of edges a full graph can have, since we have to take into account every possible connection). So have build the \(tn(3-1)=3\) matrices like:
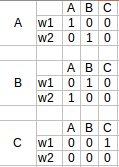 The first matrix is built in a way that we place our vector \(w\) over the nodes. Since we start with node A and put weight \(w1\) (the first value of \(w\)) on it and since A and A are in the same neighbourhood we can place a 1 to A/w1. Further since we still placed w1 to a node we set all remaining cells in the first row to zero. The second row follows from the first, since we placed w1 on A and from A to B is an edge we can only place w2 on B. We don’t have any other opportunities. For the second matrix we check node B and see how we can place the weights starting from B. The last is the same method but since we only have one node we can only place the weights on this one node and cant create any other convolution relation.
The first matrix is built in a way that we place our vector \(w\) over the nodes. Since we start with node A and put weight \(w1\) (the first value of \(w\)) on it and since A and A are in the same neighbourhood we can place a 1 to A/w1. Further since we still placed w1 to a node we set all remaining cells in the first row to zero. The second row follows from the first, since we placed w1 on A and from A to B is an edge we can only place w2 on B. We don’t have any other opportunities. For the second matrix we check node B and see how we can place the weights starting from B. The last is the same method but since we only have one node we can only place the weights on this one node and cant create any other convolution relation.
Since the first term in the formula above is a tensor product from a vector and some matrices (in our case 3) it results for every matrix in a vector (in this case its a simple vector x matrix multiplication). The three vectors are:
\(v_1 = (2, 1, 0)\), \(v_2 = (1, 2, 0)\) and \(v_3 = (0, 0, 1)\). From this we build the resulting block column vector:
\(e = \left(\begin{array}{cc}(2, 1, 0)\\ (1, 2, 0)\\ (0, 0, 1)\end{array}\right)\) which results in the matrix: \(e = \left(\begin{array}{cc}2 & 1 & 0\\ 1 & 2 & 0\\ 0 & 0 & 1\end{array}\right)\).
This resulting matrix is going to be multiplied with the data entry \(e\) as it is described in the basic formula above. This results in the vector:
\(C(e) = \left(\begin{array}{cc}13\\ 15\\ 1\end{array}\right)\)
These numbers here are only for illustrating the function! As we presented here an approach for generalizing ConvNets to irregular domains.